11 Analiza zależności cech
Jeśli badaniu statystycznemu podlega jednocześnie wiele cech, to jednym z podstawowych zagadnień staje się analiza zależności pomiędzy nimi.
Do wykrycia zależności pomocne są odpowiednie wykresy, współczynniki mierzące jej siłę oraz testy badające jej istotność.
Zmienne jakościowe
Niech zmienna \(X\) przyjmuje wartości ze zbioru \(\{x_1,\ldots x_r\}\), a zmienna \(Y\) przyjmuje wartości ze zbioru \(\{y_1,\ldots y_s\}\).
Przyjmijmy następujące oznaczenia: \[p_{ij}=P(X=x_i,Y=y_j)\quad -\quad\text{prawdopodobieństwa łączne},\] \[p_{i\cdot}=P(X=x_i),\ p_{\cdot j}=P(Y=y_j)\quad -\quad\text{prawdopodobieństwa brzegowe}.\]
Zestawiamy liczebności obserwowane w tabeli (dwudzielczej).
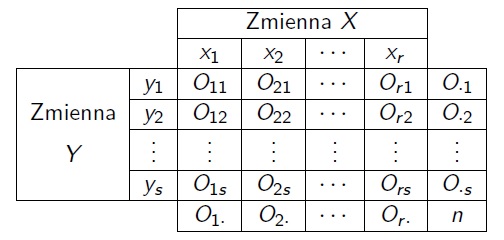
Estymatorami prawdopodobieństw są statystyki:
\[\hat p_{ij}=\frac{O_{ij}}{n},\] \[\hat p_{i\cdot}=\frac{O_{i\cdot}}{n},\ \hat p_{\cdot j}=\frac{O_{\cdot j}}{n}.\]
Zmienne \(X\) i \(Y\) są niezależne, gdy dla dowolnego \(i\) oraz \(j\): \[p_{ij}=p_{i\cdot}p_{\cdot j}.\]
Przy założeniu niezależności zmiennych liczebności oczekiwane wyliczamy ze wzoru: \[E_{ij}=n\hat p_{i\cdot}\hat p_{\cdot j}=\frac{O_{i\cdot}O_{\cdot j}}{n}.\]
Test niezależności w tablicy dwudzielczej
Założenie: Duża próba (\(n\geq 50\)).
Hipoteza zerowa: Zmienne \(X\) i \(Y\) nie są istotnie zależne. \[H_0:\ p_{ij}=p_{i\cdot}p_{\cdot j}, i=1,\ldots ,r,\ j=1,\ldots ,s.\]
Hipoteza alternatywna: Zmienne \(X\) i \(Y\) są istotnie zależne. \[H_1:\ \neg H_0\]
Statystyka testowa: \[\chi^2=\sum_{i,j}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}.\]
Rozkład statystyki testowej: \[\chi^2|_{H_0}\sim \chi^2((r-1)(s-1))\ \rm (graniczny).\]
Współczynnik niezależności \(V\)-Cramera
\[V=\sqrt{\chi ^2(\pmb{x},\pmb{y})\over n\min (r-1,s-1)},\ 0\leq V\leq 1.\]
Uwaga Oznaczenia jak w teście niezależności w tablicy dwudzielczej.
Zmienne ilościowe
Niech \(X\) i \(Y\) będą badanymi cechami populacji. O rozkładzie populacji zakładamy, że ma dwuwymiarowy rozkład normalny o gęstości: \[f(x,y)=\frac{1}{2\pi\sigma_x\sigma_y\sqrt{1-\rho^2}}\times\] \[\times\exp\left\{-\frac{1}{2(1-\rho^2)}\left[ \frac{(x-\mu_x)^2}{\sigma_x^2}-2\rho\frac{(x-\mu_x)(y-\mu_y)}{\sigma_x\sigma_y}+\frac{(y-\mu_y)^2}{\sigma_y^2}\right]\right\},\] gdzie \[\mu_x=E(X),\ \mu_y=E(Y),\ \sigma_x^2=Var(X),\ \sigma_y^2=Var(Y),\ \rho=Corr(X,Y).\]
FAKT
- \(-1\leq \rho\leq 1.\)
- Jeżeli zmienne losowe \(X\) i \(Y\) są niezależne, to \(\rho=0\).
- Jeżeli zmienne losowe \(X\) i \(Y\) mają dwuwymiarowy rozkład normalny i \(\rho=0\), to zmienne losowe \(X\) i \(Y\) są niezależne.
FAKT
Estymatorem największej wiarogodności współczynnika korelacji liniowej \(\rho\) jest statystyka:
\[\hat\rho=r={\sum _{k=1}^n(X_k-\bar X)(Y_k-\bar Y)\over \sqrt{\sum _{k=1}^n(X_k-\bar X)^2\sum _{k=1}^n(Y_k-\bar Y)^2}}, \ -1\leq r\leq 1.\]
Test istotności dla współczynnika korelacji
Założenie: Dwuwymiarowy model normalny.
Hipoteza zerowa: \[H_0:\ \rho=0\]
Hipotezy alternatywne: \[H_1:\ \rho\not =0\] \[H_1:\ \rho>0\] \[H_1:\ \rho<0\]
Statystyka testowa: \[t={r\over \sqrt{1-r^2}}\sqrt{n-2}.\]
Rozkład statystyki testowej: \[t|_{H_0}\sim t(n-2).\]
Funkcje związane z analizą zależności i korelacji cech:
chisq.test - test niezależności chi-kwadrat Pearsona,
assocstats(vcd) - współczynnik V-Cramera,
cor - współczynnik korelacji liniowej \(r\)-Pearsona,
cor.test - test istotności współczynnika korelacji liniowej.
11.1 Wywołania w R
Dane jakościowe
load("Leczenie.RData")
attach(Leczenie)
liczebnosc <- table(Efekt,Metoda)
procent <- prop.table(liczebnosc,2)*100
chisq.test(Efekt,Metoda)
library(vcd)
assocstats(liczebnosc)Dane ilościowe - model normalny