9 Regresja
Głównym celem analizy regresji jest wyznaczenie funkcji opisującej (w przybliżeniu) zależność pomiędzy zmienną niezależną - objaśniającą (lub wieloma zmiennymi niezależnymi – objaśniającymi), a zmienną zależną - objaśnianą.
Przyjmujemy następujący model:
\[Y_i=f(x_{i1},x_{i2},\ldots ,x_{im})+\varepsilon _i,\quad i=1,\ldots ,n,\]
gdzie
\(f(x_1,x_2,\ldots ,x_m)\) - funkcja regresji,
\(\varepsilon_i\) - błędy (reszty).
Założenia analizy regresji
- Niezależność obserwacji dla poszczególnych jednostek eksperymentalnych.
- Brak błędu systematycznego.
- Jednakowa i stała wariancja błędów.
- Brak korelacji błędów.
Uwaga: W procedurach testowych oraz w przypadku wykorzystywania przedziału predykcji, potrzebne jest dodatkowe założenie normalności błędów. Powoduje ono, że brak korelacji błędów oznacza ich niezależność.
Metody estymacji funkcji regresji:
Parametryczne - zakładamy znajomość postaci funkcji regresji z dokładnością do skończonej (zazwyczaj małej) liczby parametrów. W tym przypadku, do estymacji funkcji regresji używamy najczęściej metody najmniejszych kwadratów polegającej na minimalizacji wyrażenia: \[\sum _{i=1}^n\varepsilon _i^2=\sum _{i=1}^n[y_i-f(x_{i1},x_{i2},\ldots ,x_{im})]^2.\]
Nieparametryczne - nie zakładamy żadnej konkretnej postaci funkcji regresji, a do jej estymacji wykorzystujemy np. metodę jądrową.
Regresja prosta liniowa
\(X\) - zmienna niezależna (objaśniająca),
\(Y\) - zmienna zależna (objaśniana).
Model:
\[Y_i=a+bx_i+\varepsilon _i,\quad i=1,\ldots ,n,\]
gdzie
\(a, b\) - parametry liniowej funkcji regresji,
\(\varepsilon_i\) - błędy (reszty).
FAKT
Estymatorami najmniejszych kwadratów (ENK) parametrów \(a\) i \(b\) liniowej funkcji regresji są statystyki: \[\hat a=\bar Y-\hat b \bar x,\ \hat b={\sum _{i=1}^n(x_i-\bar x)(Y_i-\bar Y)\over \sum _{i=1}^n(x_i-\bar x)^2}.\]
TAKT
W modelu prostej regresji liniowej, statystyki \(\hat a\) i \(\hat b\) są nieobciążonymi estymatorami parametrów \(a\) i \(b\).
Ponadto, statystyka \[\hat{\sigma^2}=S^2=\frac{1}{n-2}\sum_{i=1}^n(Y_i-\hat a-\hat bx_i)^2\] jest nieobciążonym estymatorem parametru \(\sigma^2\).
TWIERDZENIE
Przy dodatkowym założeniu normalności rozkładu błędów, w modelu prostej regresji liniowej, statystyki \[\hat a\quad \mathrm{i} \quad S^2\quad \mathrm{oraz}\quad \hat b\quad \mathrm{i} \quad S^2\] są niezależnymi zmiennymi losowymi.
Ponadto \[\hat a\sim N\left(a,\sigma^2\left(\frac{\sum_{i=1}^nx_i^2}{n\sum_{i=1}^n(x_i-\bar x)^2}\right)\right),\] \[\hat b\sim N\left(b,\sigma^2\left(\frac{1}{\sum_{i=1}^n(x_i-\bar x)^2}\right)\right)\] oraz \[\frac{(n-2)S^2}{\sigma^2}\sim \chi^2(n-2).\]
Dopasowanie modelu
Liczbową miarą dopasowania prostej regresji do danych empirycznych jest współczynnik determinacji (podawany w %)
\[R^2=1-{SSE\over SST},\]
gdzie \[SST=\sum _{i=1}^n(Y_i-\bar Y)^2,\ SSE=\sum _{i=1}^n(\hat Y_i-Y_i)^2,\ \hat Y_i=\hat a+\hat bx_i.\]
Prognozowanie (predykcja)
Niech \(x_p\) oznacza wartość zmiennej niezależnej \(X\) dla której uzyskać chcemy prognozę zmiennej zależnej \(Y\) równą \(Y_p\).
Przyjmujemy: \[\hat{Y}_p=\hat a+\hat bx_p.\] Ponadto,
\((1-\alpha )\cdot 100\%\) przedział predykcji dla \(Y_p\) (przy założeniu normalności rozkładu błędów):
\[(\hat{Y}_p-t(1-{\alpha \over 2},n-2)S_p,\hat{Y}_p+t(1-{\alpha \over 2},n-2)S_p),\] gdzie \[S_p=S\sqrt{1+\frac{1}{n}+\frac{(x_p-\bar x)^2}{\sum_{i=1}^n(x_i-\bar x)^2}}.\]
Testy dla parametrów funkcji regresji
Hipoteza zerowa \(a\): wyraz wolny nie jest istotnie różny od zera (brak możliwości odrzucenia tej hipotezy skutkuje czasami przyjęciem modelu regresji bez wyrazu wolnego).
\[H_0:\ a=0,\ H_1:\ a\neq 0.\]
Statystyka testowa: \[t={\hat a\over S_a},\ S_a=S\sqrt{{1\over n}+ {\bar x^2\over \sum _{k=1}^n(x_k-\bar x)^2}}.\]
Rozkład statystyki testowej (przy założeniu normalności rozkładu błędów): \[t|_{H_0}\sim t(n-2).\]
Hipoteza zerowa \(b\): współczynnik kierunkowy nie jest istotnie różny od zera, tzn. zmienna niezależna \(X\) nie ma istotnego wpływu na zmienną zależną \(Y\).
\[H_0:\ b=0,\ H_1:\ b\neq 0.\]
Statystyka testowa: \[t={\hat b\over S_b},\ S_b=S\sqrt{1\over \sum _{k=1}^n(x_k-\bar x)^2}.\]
Rozkład statystyki testowej (przy założeniu normalności rozkładu błędów): \[t|_{H_0}\sim t(n-2).\]
Wpływ zmiennej niezależnej \(X\) na zmienną zależną \(Y\)
- Brak istotnego wpływu, \(b=0\).
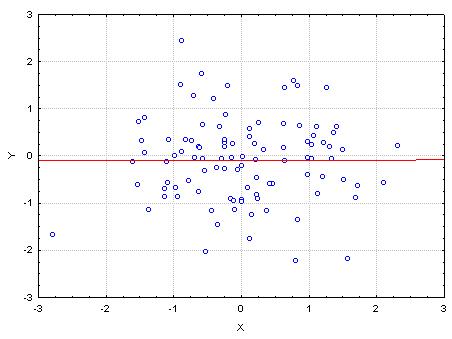
- Istotny wpływ, \(b\neq 0\).
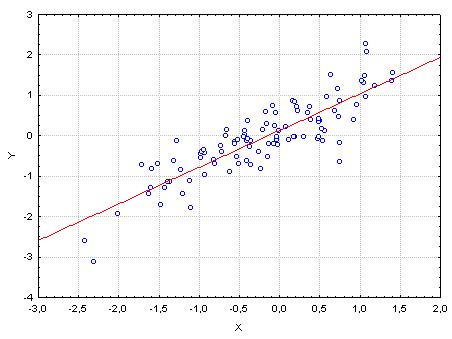
Regresja wielokrotna (wieloraka) liniowa
\(X_1,X_2,\ldots ,X_m\) - zmienne niezależne (objaśniające),
\(Y\) - zmienna zależna (objaśniana).
Model:
\[Y_i=a_0+a_1x_{i1}+a_2x_{i2}+\cdots +a_mx_{im}+\varepsilon _i,\quad i=1,\ldots ,n,\]
gdzie
\(a_0, a_1,\ldots ,a_m\) - parametry liniowej funkcji regresji,
\(\varepsilon_i\) - błędy (reszty).
Zapis macierzowy.
\[\boldsymbol{Y}=\left [ \begin{array}{c} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{array} \right ],\quad \boldsymbol{X}=\left [ \begin{array}{cccc} 1 & x_{11} & \ldots & x_{1m} \\ 1 & x_{21} & \ldots & x_{2m} \\ \vdots & \vdots & & \vdots \\ 1 & x_{n1} & \ldots & x_{nm} \end{array} \right ],\quad \boldsymbol{a}=\left [ \begin{array}{c} a_0 \\ a_1 \\ \vdots \\ a_m \end{array} \right ].\quad \boldsymbol{\varepsilon }=\left [ \begin{array}{c} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{array} \right ] \]
Model liniowy:
\[\boldsymbol{Y}=\boldsymbol{X}\boldsymbol{a}+\boldsymbol{\varepsilon}.\]
Dodatkowe założenia i estymatory parametrów
Dodatkowe założenia wynikające z używania \(m>1\) zmiennych niezależnych:
- Liczebność próby jest większa od liczby szacowanych parametrów, tzn. \(n>m+1\).
- Pomiędzy wektorami obserwacji zmiennych objaśniających nie istnieje zależność liniowa. Warunek ten oznacza, że \[\text{rząd}(\pmb X)=m+1.\]
FAKT
Estymatory parametrów funkcji regresji} uzyskane metodą najmniejszych kwadratów maja postać:
\[\boldsymbol{\hat a}=\boldsymbol{(X'X)^{-1}X'Y}.\]
FAKT
W modelu wielokrotnej regresji liniowej, statystyka \[\boldsymbol{\hat a}=\boldsymbol{(X'X)^{-1}X'Y}\] jest nieobciążonym estymatorem parametru \(\boldsymbol{\hat a}\).
Ponadto, statystyka \[\hat{\sigma^2}=S^2=\frac{1}{n-m-1}\sum_{i=1}^n(Y_i-\hat Y_i)^2,\] gdzie \[\hat Y_i=\hat a_0+\hat a_1x_{i1}+\cdots +\hat a_mx_{im},\quad i=1,\ldots ,n,\] jest nieobciążonym estymatorem parametru \(\sigma^2\).
Dopasowanie modelu
Liczbową miarą dopasowania hiperpłaszczyzny regresji do danych empirycznych jest współczynnik determinacji (podawany w %) \[R^2=1-{SSE\over SST},\] gdzie \[SST=\sum _{i=1}^n(Y_i-\bar Y)^2,\ SSE=\sum_{i=1}^n(\hat Y_i-Y_i)^2,\] \[\hat Y_i=\hat a_0+\hat a_1x_{i1}+\cdots +\hat a_mx_{im},\quad i=1,\ldots ,n.\]
W przypadku wielu zmiennych niezależnych stosujemy poprawiony współczynnik determinacji \[R^2_{pop}=1-{SSE/(n-m-1)\over SST/(n-1)}.\]
Prognozowanie (predykcja)
Niech \(\pmb X_p\) oznacza wektor wartości zmiennych objaśniających dla której uzyskać chcemy prognozę zmiennej objaśnianej \(Y_p\).
Dokładnie: \[\pmb X_p=\left[ \begin{array}{c} 1 \\ x_1^p \\ \vdots \\ x_m^p \\ \end{array} \right].\]
Przyjmujemy: \[\hat{Y}_p=\pmb X_p'\hat{\pmb a}.\]
Ponadto,
\((1-\alpha )\cdot 100\%\) przedział ufności dla \(Y_p\) (przy założeniu normalności rozkładu błędów):
\[(\hat{Y}_p-t(1-{\alpha \over 2},n-m-1)S_p,\hat{Y}_p+t(1-{\alpha \over 2},n-m-1)S_p),\] gdzie \[S_p^2=S^2(1+\pmb{X}_p'(\pmb{X}'\pmb{X})^{-1}\pmb{X}_p).\]
Analiza wariancji w regresji
Hipoteza zerowa: żaden ze współczynników \(a_1,\ldots ,a_m\) nie jest istotnie różny od zera, tzn. żadna zmienna niezależna \(X_1,\ldots X_m\) nie ma istotnego wpływu na zmienną zależną \(Y\). \[H_0:\ a_1=a_2=\cdots =a_m=0\]
Hipoteza alternatywna: \[H_1:\ \neg H_0.\]
Statystyka testowa:
\[F_R={SSR\over m}/{SSE\over n-m-1}\]
Uwaga! \(SST=SSR+SSE\), gdzie \(SST=\sum _{i=1}^n(Y_i-\bar Y)^2\), \(SSR=\sum _{i=1}^n(\hat Y_i-\bar Y)^2\), \(SSE=\sum _{i=1}^n(\hat Y_i-Y_i)^2\).
Rozkład statystyki testowej (przy założeniu normalności błędów): \[F_R|_{H_0}\sim F(m,n-m-1).\]
Tabela analizy wariancji w regresji
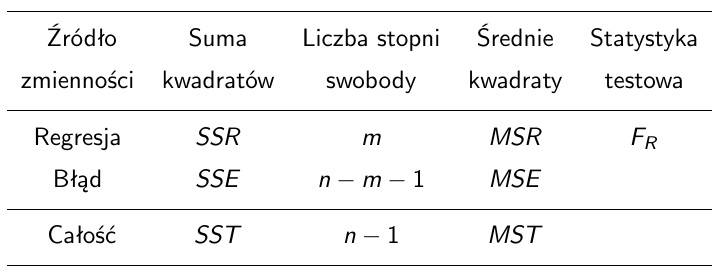
\[MSR=SSR/m,\ MSE=SSE/(n-m-1),\ MST=SST/(n-1).\]
Testowanie istotności parametrów modelu
Hipotezy: \(H_0:\ a_j=0,\ H_1:\ a_j\neq 0,\ j=1,2,\ldots ,m.\)
Statystyka testowa: \[t_j={\hat a_j\over S_{a_j}},\] gdzie \[S^2_{a_j}=MSE\cdot d_{jj}\] oraz \(d_{jj}\) jest \(j\)-tym elementem głównej przekątnej macierzy \((\pmb X'\pmb X)^{-1}\).
Rozkład statystyki testowej (przy założeniu normalności rozkładu błędów): \[t_j|_{H_0}\sim t(n-m-1).\]
Regresja nieliniowa
Metody szacowania parametrów modelu:
- linearyzacja - polega na przekształceniu modelu nieliniowego do modelu liniowego, poprzez transformację zmiennych niezależnych lub/i zmiennej zależnej. Przykładowo, model Cobba-Douglasa postaci \[y=a_0x_{1}^{a_1}x_{2}^{a_2},\] można przekształcić do modelu liniowego poprzez transformację \(y'=\ln(y)\), \(x_1'=\ln(x_1)\), \(x_2'=\ln(x_2)\) oraz \(a_0'=\ln(a_0)\).
Wtedy
\[y'=a_0'+a_1x_{1}'+a_2x_{2}'.\]
- numeryczne rozwiązanie zagadnienia minimalizacji sumy kwadratów błędów.
Regresja logistyczna
W regresji logistycznej badamy wpływ \(m\) niezależnych zmiennych \(X_1,\ldots ,X_m\) (ilościowych) na zależną zmienną \(Y\) mającą charakter dychotomiczny (zero-jedynkowy).
Model
\[p=E(Y|\pmb X=\pmb x)=\frac{\exp(a_0 +a_1 x_{1}+\cdots +a_m x_{m})}{1+\exp(a_0 +a_1 x_{1}+\cdots +a_m x_{m})},\] gdzie
\(p\) - prawdopodobieństwo sukcesu,
\(a_0,a_1,\ldots ,a_m\) - współczynniki regresji.
Krzywa logistyczna
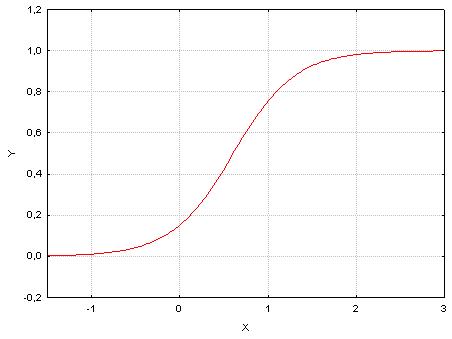
- Współczynniki regresji \(a_0,a_1,\ldots ,a_m\) estymujemy metodą największej wiarogodności wykorzystując iteracyjny algorytm IWLS (algorytm iteracyjnie ważonych najmniejszych kwadratów).
- Wielkość \[\ln\frac{p}{1-p}=a_0 +a_1 x_{1}+\cdots +a_m x_{m}\] nazywamy logitem.
- Wielkość \[\frac{p}{1-p}=\exp(a_0 +a_1 x_{1}+\cdots +a_m x_{m})\] nazywamy ilorazem szans.
Funkcje związane z analizą regresji:
lm - regresja liniowa, procedura główna,
nls - regresja nieliniowa, procedura główna,
glm - regresja logistyczna, procedura główna,
predict - prognozowanie.
9.1 Wywołania w R
Regresja liniowa prosta
Wybór modelu:
Estymacja parametrów (testy istotności dla parametrów):
Prognoza dla Girth=11.5:
Wykres dopasowanej funkcji regresji:
Przedziały ufności:
prognoza1 <- predict(reg,list(Girth=11.5),interval='confidence')
prognoza1
prognoza2 <- predict(reg,list(Girth=11.5),interval='prediction')
prognoza2Wykres z przedziałami ufności:
plot(Girth,Volume)
abline(reg,col='red')
new <- seq(min(Girth),max(Girth),length=100)
prognoza1 <- predict(reg,list(Girth=new),interval='confidence')
lines(new,prognoza1[,2],lty=2,col='blue')
lines(new,prognoza1[,3],lty=2,col='blue')
prognoza2 <- predict(reg,list(Girth=new),interval='prediction')
lines(new,prognoza2[,2],lty=2,col='green')
lines(new,prognoza2[,3],lty=2,col='green')Regresja liniowa wielokrotna
Estymacja parametrów (testy istotności dla parametrów):
Prognoza dla Girth=11.5, Height=75:
predict(reg,list(Girth=11.5,Height=75))
predict(reg,list(Girth=11.5,Height=75),interval='confidence')
predict(reg,list(Girth=11.5,Height=75),interval='prediction')load("Peru.RData")
attach(Peru)
reg <- lm(BP~age+years+weight+height)
summary(reg)
reg <- lm(BP~.,data=Peru)
summary(reg)Regresja nieliniowa prosta
Linearyzacja
load("Wydatki.RData")
attach(Wydatki)
plot(Doch,Wyd)
y <- 1/Wyd
x <- 1/Doch
plot(x,y)
reg <- lm(y~x)
summary(reg)
par <- coef(reg)
a <- 1/par[1]
b <- par[2]/par[1]
plot(Doch,Wyd)
x <- seq(min(Doch),max(Doch),length=100)
lines(x,(a*x)/(x+b),col='red')Minimalizacja sumy kwadratów reszt.
reg <- nls(Wyd~(a*Doch)/(Doch+b),start=list(a=1,b=-0.75))
summary(reg)
par <- coef(reg)
aa <- par[1]
bb <- par[2]
plot(Doch,Wyd)
x <- seq(min(Doch),max(Doch),length=100)
lines(x,(a*x)/(x+b),col='red')
lines(x,(aa*x)/(x+bb),col='green')Regresja logistyczna