6 Testy statystyczne
Hipotezy statystyczne
Tradycyjnie, niech \(\theta\) oznacza parametr modelu statystycznego.
Dotychczasowe rozważania dotyczyły metod estymacji tego parametru (punktowej lub przedziałowej). Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę mówiącą, że jego “prawdziwa” wartość nie różni się istotnie od zadanej wartości, co zapisujemy: \(\theta =\theta_0\), gdzie \(\theta_0\) jest ustalone.
Poza samą hipotezą (nazywać ją będziemy hipotezą zerową) musimy jeszcze podać hipotezę alternatywną, czyli ustalić jaka jest nasza decyzja w przypadku odrzucenia hipotezy zerowej.
Przykładowo, dla hipotezy zerowej \(H_0:\ \theta=\theta_0\), możliwe są następujące alternatywy: \(H_1:\ \theta \not =\theta_0\), \(H_1:\ \theta >\theta_0\) lub \(H_1:\ \theta <\theta_0\).
Przykłady układów hipotez
Hipoteza zerowa: wartość oczekiwana (średnia) badanej cechy nie różni się istotnie od 20.
Hipoteza alternatywna: wartość oczekiwana (średnia) badanej cechy jest istotnie większa od 20.
Hipoteza zerowa: wartości oczekiwane (średnie) badanej cechy w dwóch grupach nie różnią się istotnie.
Hipoteza alternatywna: wartości oczekiwane (średnie) badanej cechy w dwóch grupach różnią się istotnie.
Hipoteza zerowa: nie ma istotnej zależności pomiędzy dwoma badanymi cechami.
Hipoteza alternatywna: istnieje istotna zależność pomiędzy dwoma badanymi cechami.
Obszary krytyczne
Konstruując procedurę testową wyznaczamy tzw. obszar krytyczny (obszar odrzuceń hipotezy zerowej). Najbardziej typowym jest prawostronny obszar krytyczny postaci:
\[R=\{ \mathbf{x}:\ T(\mathbf{x})\geq k\},\] gdzie \(T\) jest statystyką testową, a \(k\) oznacza wartość krytyczną.
Stąd jeśli wartość statystyki testowej jest duża (przekracza wartość krytyczną), to odrzucamy hipotezę zerową.
Inne postaci obszarów krytycznych:
- Lewostronny obszar krytyczny: \[R=\{\ \mathbf{x}\in {\cal X}:\ T(\mathbf{x})\leq k\ \},\]
- Dwustronny obszar krytyczny: \[R=\{\ \mathbf{x}\in {\cal X}:\ T(\mathbf{x})\geq k_1\ {\rm lub}\ T(\mathbf{x})\leq k_2\ \},\]
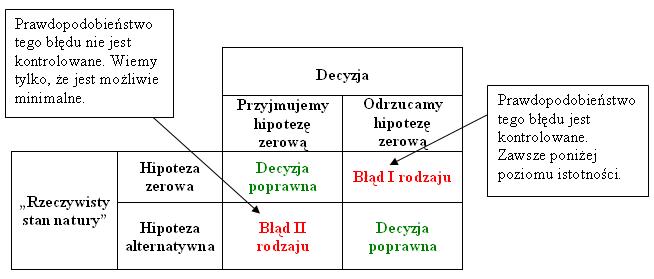
Błędy pierwszego i drugiego rodzaju
Przyjmując lub odrzucając hipotezę zerową podejmujemy decyzję, która może być poprawna lub błędna.
Podczas testowania hipotezy zerowej możemy popełnić jeden z dwóch następujących błędów.
Odrzucamy hipotezę zerową gdy jest ona prawdziwa - błąd I rodzaju.
Przyjmujemy hipotezę zerową gdy jest ona fałszywa - błąd II rodzaju.
Wybór wartości krytycznej
Ustalamy poziom istotności testu \(\alpha\) i dobieramy wartość krytyczną tak, aby
prawdopodobieństwo popełnienia błędu I rodzaju było mniejsze lub równe \(\alpha\),
prawdopodobieństwo popełnienia błędu II rodzaju było minimalne.
Wynik testowania hipotez
Ponieważ decyzja przyjęcia hipotezy zerowej może pociągnąć za sobą popełnienie błędu II rodzaju (prawdopodobieństwo tego błędu nie jest kontrolowane i nawet w najlepszych testach może być bardzo duże), to wynikiem testowania hipotez jest jedna z dwóch decyzji:
“odrzucamy hipotezę zerową” tzn. stwierdzamy występowanie istotnych statystycznie różnic (zależności), na poziomie istotności \(\alpha\),
“nie ma podstaw do odrzucenia hipotezy zerowej”, tzn. nie stwierdzamy występowania istotnych statystycznie różnic (zależności), na poziomie istotności \(\alpha\).
\(p\)-wartość
DEFINICJA
\(p\)-wartość jest najmniejszym poziomem istotności testu, przy którym odrzucamy hipotezę zerową.
WNIOSEK
- Jeżeli \(p\)–wartość $$, to odrzucamy \(H_0\).
- Jeżeli \(p\)–wartość $>$, to nie ma podstaw do odrzucenia \(H_0\).
Sposób obliczania \(p\)-wartości
Prawostronny obszar krytyczny: \[{\rm P}_0(T\geq T(\mathbf{x})).\]
Lewostronny obszar krytyczny: \[{\rm P}_0(T\leq T(\mathbf{x})).\]
Dwustronny obszar krytyczny: \[2\min \{\ {\rm P}_0(T\geq T(\mathbf{x})),\ {\rm P}_0(T\leq T(\mathbf{x}))\ \}.\]
Testy ilorazu wiarogodności
Załóżmy, że dysponujemy \(n\)-elementową próbą, a \(\theta\) oznacza parametr modelu statystycznego. Rozważamy zagadnienie testowania układu hipotez: \[H_0:\ \theta\in\Theta_0,\] \[H_1:\ \theta\in \Theta_1,\ \Theta_0\cup \Theta_1=\Theta,\ \Theta_0\cap \Theta_1=\varnothing .\] Ponadto załóżmy, że populacja, z której pochodzi nasza próba ma rozkład absolutnie ciągły.
DEFINICJA
Testem ilorazu wiarogodności nazywamy test z obszarem krytycznym postaci: \[R=\{ \mathbf{x}:\ \frac{\sup_{\theta\in\Theta}L(\theta ;\mathbf{x})}{\sup_{\theta\in\Theta_0}L(\theta ;\mathbf{x})}\geq k_{\alpha}\},\] gdzie wartość krytyczną \(k_{\alpha}\) wyznaczamy tak, aby prawdopodobieństwo błędu pierwszego rodzaju było równe \(\alpha\).
Przykład.
Załóżmy, że dysponujemy \(n\)-elementową próbą prostą \(\pmb X=(X_1,X_2,\ldots ,X_n)'\) z populacji o rozkładzie wykładniczym z parametrem \(\lambda\).
Obszar krytyczny testu ilorazu wiarogodności dla układu hipotez:\[H_0: \lambda=\lambda_0\] \[H_1: \lambda<\lambda_0\] ma następującą postać: \[R=\{ \mathbf{x}:\ 2\lambda_0n\bar x\geq \chi^2(1-\alpha,2n) \}.\]