8 ANOVA
Jednoczynnikowa ANOVA
Na test jednoczynnikowej analizy wariancji możemy patrzeć jak na uogólnienie testu \(t\) Studenta dla dwóch prób niezależnych, na przypadek \(k\), \((k>2)\) prób niezależnych.
Model
\[X_{ij}=\mu _{i}+\varepsilon _{ij},\ i=1,\ldots ,k,\ j=1,\ldots ,n_i,\]
gdzie
\(\mu _{i}\) - “prawdziwa” wartość badanej cechy i \(i\)-tej grupie,
\(\varepsilon _{ij}\) - błędy (niezależne zmienne losowe o jednakowym rozkładzie \(N(0,\sigma^2 )\)).
Hipoteza zerowa: wartości oczekiwane (średnie) badanej cechy w \(k\) grupach nie różnią się istotnie: \[H_0:\ \mu _1=\mu _2=\cdots =\mu _k.\]
Hipoteza alternatywna: co najmniej dla jednej pary grup, wartości oczekiwane (średnie) badanej cechy różnią się istotnie: \[H_1:\ \neg H_0.\]
Statystyka testowa: \[F={SSA\over k-1}/{SSE\over n-k},\] gdzie \[SSA=\sum _{i=1}^kn_i(\bar X_{i.}-\bar X_{..})^2,\quad SSE=\sum _{i=1}^k\sum _{j=1}^{n_i}(X_{ij}-\bar X_{i.})^2,\] \[\bar X_{i.}={1\over n_i}\sum_{j=1}^{n_i}X_{ij},\ \bar X_{..}={1\over n}\sum _{i=1}^k\sum _{j=1}^{n_i}X_{ij},\ n=\sum_{i=1}^kn_i.\]
Rozkład statystyki testowej: \[F|_{H_0}\sim F(k-1,n-k)\]
Tabela analizy wariancji
Tradycyjnie wyniki analizy wariancji przedstawiamy w postaci tabeli.
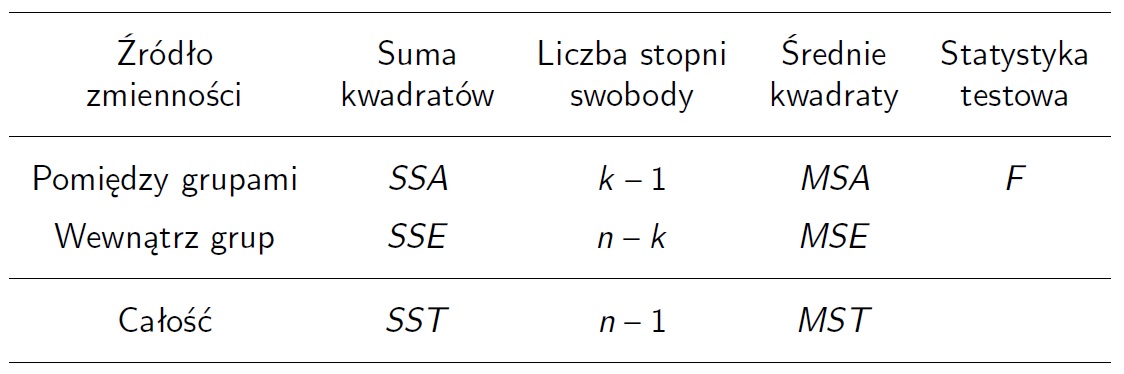
\[MSA=SSA/(k-1),\ MSE=SSE/(n-k),\ MST=SST/(n-1).\]
Założenia jednoczynnikowej analizy wariancji
- Niezależność obserwacji dla poszczególnych jednostek eksperymentalnych.
- Błędy mają rozkłady normalne z zerową wartością oczekiwaną (brak błędu systematycznego) i jednorodną wariancją.
Uwaga: Założenie jednorodności wariancji błędów możemy zweryfikować testem Bartletta.
Test Bartletta
Założenia: Model normalny, wiele prób niezależnych.
Hipoteza zerowa: \[H_0:\ \sigma _1^2=\sigma _2^2=\cdots =\sigma _k^2\]
Hipoteza alternatywna: \[H_1:\ \neg H_0\]
Statystyka testowa: \[B={1\over C}(n-k)\ln MSE-\sum _{i=1}^k(n_i-1)\ln S_i^2,\] gdzie \[C=1+{1\over 3(k-1)}\Bigl [\sum_{i-1}^k{1\over n_i-1}-{1\over n-k }\Bigr ].\]
Rozkład statystyki testowej: \[B|_{H_0}\sim \chi ^2(k-1),\ \rm (graniczny)\]
Porównania wielokrotne (post hoc)
Procedury porównań wielokrotnych stosujemy wtedy, gdy zostanie odrzucona hipoteza zerowa w analizie wariancji!!!
Procedura NIR – Fishera.
Polega na testowaniu, dla każdej pary \((i,j)\), \(i,j=1,2,\ldots ,k\), \(i\neq j\), oddzielnie hipotezy zerowej: \[H_0:\ \mu_{i}=\mu_{j},\] przeciwko hipotezie alternatywnej \[H_1:\ \mu_{i}\neq\mu_{j}.\]
Wartość statystyki testowej obliczamy ze wzoru: \[t=\frac{\bar x_{i.}-\bar x_{j.}}{\sqrt{MSE}}\sqrt{\frac{n_{i}n_{j}}{n_{i}+n_{j}}}.\]
Przy braku istotnych różnic statystyka ta ma rozkład \(t\) Studenta z \(n-k\) stopniami swobody.
Procedura HSD – Tukey’a.
Niech \(n_1=n_2=\cdots =n_k=m.\)
Polega na testowaniu, jednocześnie dla wszystkich par \((i,j)\), \(i,j=1,2,\ldots ,k\), \(i\neq j\), hipotez zerowych: \[H_0:\ \mu_{i}=\mu_{j},\] przeciwko hipotezom alternatywnym \[H_1:\ \mu_{i}\neq\mu_{j}.\]
Wartość statystyki testowej obliczamy ze wzoru: \[q=\frac{\bar x_{i.}-\bar x_{j.}}{\sqrt{MSE}}\sqrt{m}.\]
Przy braku istotnych różnic statystyka ta ma rozkład \(q\) (rozkład studentyzowanego rozstępu) z \(k\) i \(k(m-1)\) stopniami swobody.
Jednoczynnikowa ANOVA - układ doświadczalny
Na test jednoczynnikowej analizy wariancji możemy patrzeć jak na badanie istotności wpływu czynnika \(A\) na mającą charakter ilościowy i ciągły cechę \(X\). Czynnik występuje na \(k\) poziomach które oznaczamy \(A_1,A_2,\ldots ,A_k\). Poziomy czynnika \(A\) nazywamy obiektami doświadczalnymi.
Obiekty doświadczalne są kontrolowane przez eksperymentatora, przy czym każdy z nich jest związany z pewną liczbą jednostek doświadczalnych. Liczba jednostek doświadczalnych związana z określonym obiektem nazywana jest liczbą replikacji tego obiektu.
Kojarząc różne obiekty z jednostkami doświadczalnymi, eksperymentator kreuje różne populacje, które pragnie porównać na podstawie obserwacji badanej w doświadczeniu cechy \(X\).
Układ całkowicie losowy
\[X_{ij}=\mu +\alpha _i+\varepsilon _{ij},\quad i=1,\ldots ,k,\ j=1,\ldots ,n_i,\] gdzie
\(\mu\) - średnia ogólna,
\(\alpha _i\) - efekt \(i\)–tego obiektu, \(\sum _{i=1}^{k}\alpha _i=0\),
\(\varepsilon _{ij}\) - błędy (niezależne zmienne losowe o jednakowym rozkładzie \(N(0,\sigma^2 )\)).
Hipoteza zerowa: czynnik \(A\) nie ma istotnego wpływu na cechę \(X\): \[H_0:\ \alpha _1=\alpha _2=\cdots =\alpha _k.\]
Hipoteza alternatywna: czynnik \(A\) ma istotny wpływ na cechę \(X\): \[H_1:\ \neg H_0.\]
Tabela analizy wariancji
Tradycyjnie wyniki analizy wariancji przedstawiamy w postaci tabeli.
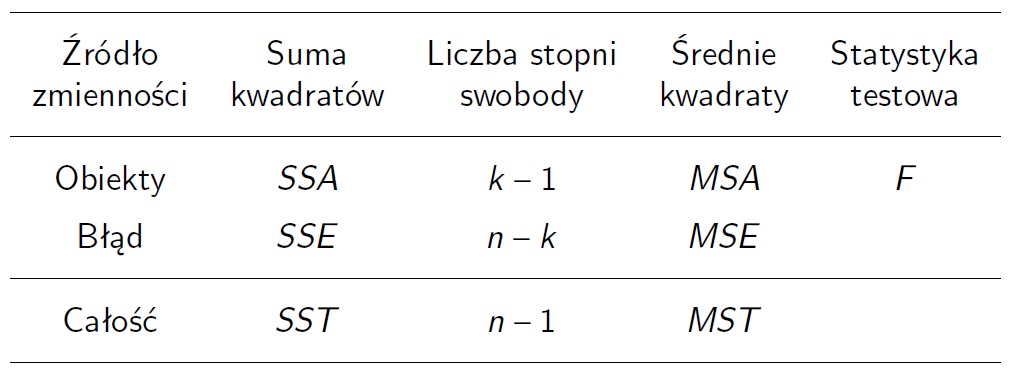
\[MSA=SSA/(k-1),\quad MSE=SSE/(n-k),\quad MST=SST/(n-1).\]
Układ losowych bloków kompletnych
W celu wyeliminowania niejednorodności jednostek eksperymentalnych możemy pogrupować je w bloki. Grupowanie to podporządkowane jest zasadzie, zgodnie z którą naturalna zmienność jednostek wewnątrz każdego bloku powinna być możliwie najmniejsza, podczas gdy zmienność jednostek pochodzących z różnych bloków może być duża. W ten sposób stwarzamy porównywanym obiektom bardziej wyrównane warunki i równocześnie ograniczamy w doświadczeniu wpływ naturalnej zmienności jednostek eksperymentalnych na wielkość wariancji błędu.
\[X_{ij}=\mu +\alpha _i+\beta _j+\varepsilon _{ij},\ i=1,\ldots ,k,\ j=1,\ldots ,b,\] gdzie
\(\mu\) - średnia ogólna,
\(\alpha _i\) - efekt \(i\)-tego obiektu, \(\sum _{i=1}^{k}\alpha _i=0\),
\(\beta _j\) - efekt \(j\)-tego bloku, \(\sum _{j=1}^{b}\beta _j=0\),
\(\varepsilon _{ij}\) - błędy (niezależne zmienne losowe o jednakowym rozkładzie \(N(0,\sigma^2 )\)).
Hipoteza zerowa: \[H_0:\ \alpha _1=\alpha _2=\cdots =\alpha _k.\]
Hipoteza alternatywna: \[H_1:\ \neg H_0.\]
Statystyka testowa: \[F={SSA}/{SSE\over b-1}\]
\[SSA=b\sum _{i=1}^k(\bar X_{i.}-\bar X_{..})^2,\ SSE=\sum _{i=1}^k\sum _{j=1}^{b}(X_{ij}-\bar X_{i.}-\bar X_{.j}+\bar X_{..})^2,\] gdzie
\[\bar X_{i.}={1\over k}\sum_{j=1}^{b}X_{ij},\ \bar X_{.j}={1\over b}\sum_{i=1}^{k}X_{ij},\ \bar X_{..}={1\over n}\sum _{i=1}^k\sum _{j=1}^{b}X_{ij},\ n=kb.\]
Rozkład statystyki testowej: \[F|_{H_0}\sim F(k-1,(k-1)(b-1))\]
Tabela analizy wariancji
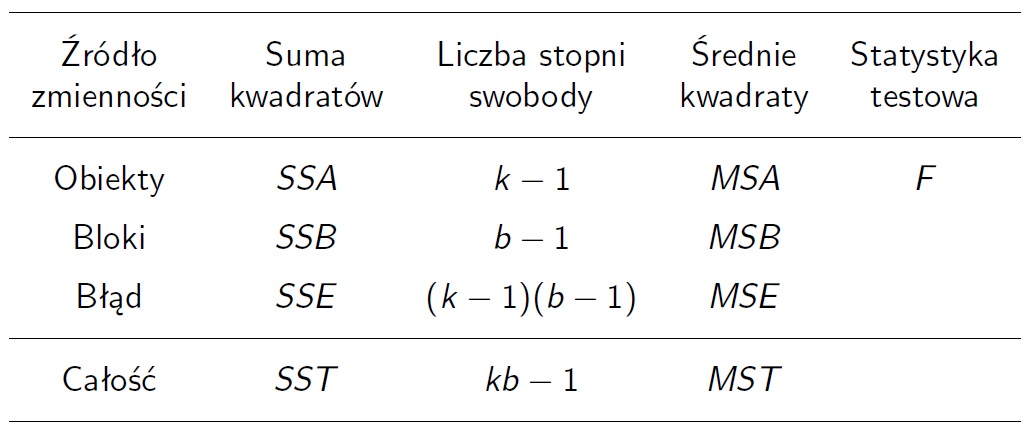
\[MSA=SSA/(k-1),\ MSB=SSB/(b-1),\ MSE=SSE/(k-1)(b-1),\] \[MST=SST/(kb-1).\]
Funkcje związane z ANOVA:
aov - procedura główna,
LSD.test(agricolae) - procedura NIR Fishera,
HSD.test(agricolae) - procedura HSD Tukeya,
bartlett.test - test Bartletta.
8.1 Wywołania w R
Układ całkowicie losowy
load("Proszki.RData")
attach(Proszki)
tapply(Wynik,Typ,mean)
ftyp <- factor(Typ)
plot.design(Wynik~ftyp)
anova <- aov(Wynik~ftyp)
summary(anova)Analiza reszt
Analiza Post-Hoc
LSD
LSD+Bonferoni
HSD
Układ losowych bloków kompletnych
load("Herbicydy.RData")
attach(Herbicydy)
fobiekty <- factor(Obiekty)
fbloki <- factor(Bloki)
tapply(Plon,fobiekty,mean)
tapply(Plon,fbloki,mean)
plot.design(data.frame(fobiekty,fbloki,Plon))
anova <- aov(Plon~fobiekty+fbloki)
summary(anova)Analiza Post-Hoc
LSD
LSD+Bonferoni
HSD